The probability of breast cancer is 13.8% for a woman with a dominant gene mutation. If a woman with a dominant gene mutation actually has breast cancer, the probability is:

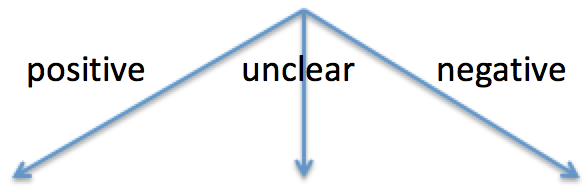
- 53.7% that she will receive a positive mammogram,
- 24.6% that she will receive an unclear result, and
- 21.7% that she will receive a negative mammogram.
If a woman with a dominant gene mutation does not have breast cancer, the probability is:
- 7.7% that she will receive a positive mammogram,
- 7.7 % that she will receive an unclear result, and
- 84.6% that she will receive a negative mammogram.

What is the probability that a woman with a dominant gene mutation actually has breast cancer, given that she has a positive mammogram?

Show answer

The probability of having disease A is 0.4% for a person without any symptoms.
The probability of having disease B is 0.1% for a person without any symptoms.
(Diseases A and B never occur at the same time.)
There is a medical test which can detect both diseases. But it is unable to discriminate between disease A and B and, furthermore, it is not safe.
- If a person has disease A, the probability is 90% that she or he will receive a positive result.
- If a person has disease B, the probability is 80% that she or he will receive a positive result.
- If a person has neither disease A nor disease B, the probability is 10% that she or he will nevertheless receive a positive result.

What is the probability that a person without any symptoms obtains a positive test result, if the person actually suffers from
- disease A?
- disease B?
- any of the diseases (A or B)?

Show answer

The probability of breast cancer is 1% for a woman at age 40 who participates in routine screening.If a woman has breast cancer,the probability is 80% that she will have a positive mammogram. If a woman does not have breast cancer,the probability is 9.6% that she will also have a positive mammogram. If a woman has breast cancer, the probability is 95% that she will have a positive ultrasound test.If a woman does not have breast cancer,the probability is 4% that she will also have a positive ultrasound test.

What is the probability that she actually has breast cancer if all 2 tests are positive?

Show answer

The probability of having a special complaint is 2%.
If a person has the complaint, the probability is 80% that she or he will receive a positive test result in test 1.
If a person has the complaint, the probability is 95% that she or he will receive a positive test result in test 2.
If a person has the complaint, the probability is 75% that she or he will receive a positive test result in test 3.
If a person does not have the complaint, the probability is 25% that she or he will nevertheless receive a positive test result in test 1.
If a person does not have the complaint, the probability is 10% that she or he will nevertheless receive a positive test result in test 2.
If a person does not have the complaint, the probability is 20% that she or he will nevertheless receive a positive test result in test 3.

What is the probability that a person actually has the complaint if all 3 tests are positive?

Show answer

Suppose you were told that a taxi-cab was involved in a hit-and-run accident one night. Of the taxi-cabs in the city, 85% belonged to the Green company and 15% to the Blue company. An eyewitness had identified the cab as a blue cab. But when her ability to identify cabs under appropriate visibility conditions was tested, she was wrong 20% of the time. What is the probability that the taxi-cab involved in the accident was blue?

Show answer

Rape case: A match was found between the DNA profile of suspect and a trace found on the victim (hardly any other evidence).

Expert statement in probabilities: There are 10 million men who fit the description of the perpetrator. The probability that the DNA profile of a randomly selected man matches the trace found on the victim is approximately 0.0001%. If a man has this DNA profile, the DNA test will almost certainly produce a match. If he does not have this DNA profile, the test will produce a match with a probability of 0.001%.

Question 1: What is the probability that the reported match is a true match, that is, that the suspect indeed has the same DNA profile as found in the trace?

Question 2: What is the probability that the suspect is the source of the trace found on the victim?

Show answer

Imagine you are the manager of a business investigating missing petty cash. Your investigation involves collecting reports from employees. It is unclear whether the cash is missing due to an error or because it was stolen, but you initially have a strong hunch that it was not stolen (you assume only a one in 3 chance of theft, i.e. a 33% chance).

During the course of your investigation, Robert (an employee) approaches you to provide a report that one of your other employees (Thomas) stole the cash. Dan, the supposed direct witness to this event, is on leave and cannot give his statement directly. However, you have confirmed that Dan was at work at the time the incident occurred. Instead Dan’s witness statement is being supplied to you via another employee. This employee, Robert, who was not present himself when the incident occurred, has come forward, reporting to you that Dan told him that he (Dan) witnessed Thomas stealing the cash.

To determine the probability that the cash was in fact stolen, you must take into account the chance of Dan’s and Robert’s statements being true or false. Both Dan and Robert are more likely to provide a true report than a false one. Specifically, there is a 90% chance that Dan’s report is true (hit rate), and only a 10% chance that his report will wrongly implicate Thomas (false positive rate). Robert’s report has a 60% chance of being true (hit rate) and a 40% chance of wrongly implicating Thomas (false positive rate).

Consider the following scenarios:

Order 1: You receive Robert’s report of what Dan claims to have seen. Imagine how convinced Robert’s report would make you that Thomas stole the cash.

Order 2: Imagine that everything about Dan and Robert stays the same except that they have swapped places, so that it is now Robert who claims to have seen Thomas, and Dan who reports on Robert’s testimony. Despite swapping places, Dan’s hit rate is still 90%, and his false positive rate is 10%, while Robert’s hit rate is 60%, and his false positive rate is 40%. Again, imagine how convinced Dan’s report would make you that Thomas stole the cash.

Question 1: Is there any difference in how convinced you (“the manager”) should be that Thomas stole the cash across these two orders?

[Please select from the following options in the study survey]

1. Order 1 provides more convincing evidence.
2. Order 2 provides more convincing evidence.
3. Order 1 and Order 2 are equally convincing.

Per company policy, you must believe that it is at least 70% likely that Thomas stole the cash to proceed with an investigation and potentially report the incident to outside authorities. Consider both of the orders presented.

Question 2: Should you (“the manager”) be sufficiently convinced (>70%) by either Order 1 or Order 2?

[Please select from the following options in the study survey]

1. I would be sufficiently convinced by Order 1.
2. I would be sufficiently convinced by Order 2.
3. I would be sufficiently convinced in both cases.
4. I would not be sufficiently convinced in either case.

Question 3: Please provide an explanation to the above two answers, using numerical calculations or diagrams if appropriate.

You should indicate, for both Order 1 and Order 2, how convinced you are that Thomas stole the cash, whether you are sufficiently convinced (greater than 70%) that Thomas stole the cash (and thus recommend investigation), and you should discuss how swapping the witnesses may impact your convictions. Better scores are likely to be obtained from a complete and well-reasoned explanation.

Imagine an alternative scenario with the same basic events as before. Instead of Dan and Robert, two different employees, Anne and Brenda, make claims that the cash was stolen by your employee Thomas.

Again, during the course of your investigation, you receive a report that one of your employees (Thomas) stole the cash. Anne, the supposed direct witness, is on leave and cannot give this statement directly. However, you have confirmed that Anne was at work at the time the incident occurred. Instead this information is being supplied to you via another employee, Brenda, who was not at work at the time the incident occurred. Brenda has come forward, reporting to you Anne’s statement that she (Anne) saw Thomas steal the cash.

To determine the probability that the cash was in fact stolen, you must take into account the chance of Anne’s and Brenda’s statements being true or false. In this version of the problem, both Anne and Brenda are very reliable in the sense that they are 10 times more likely to pass on truthful information (hit rate) than to pass on false information, whether intentionally or inadvertently, that wrongly implicates Thomas (false positive rate). To illustrate, Anne is 10 times more likely to correctly report that a theft occurred, than to falsely report that a theft occurred.

However, based on your previous interactions with Anne and Brenda you also know that both might hesitate to say anything that could get a colleague in trouble, even when that colleague has done something wrong.

Question 4: Is there any difference in how convinced you (“the manager”) should be that Thomas stole the cash across these two orders?

[Please select from the following options in the study survey]

1. Order 1 provides more convincing evidence.
2. Order 2 provides more convincing evidence.
3. Order 1 and Order 2 are equally convincing.

Per company policy, you must believe that it is at least 70% likely that Thomas stole the cash to proceed with an investigation and potentially report the incident to outside authorities. Consider both of the orders presented.

Question 5: Should you (“the manager”) be sufficiently convinced (>70%) by either Order 1 or Order 2?

[Please select from the following options in the study survey]

1. I would be sufficiently convinced by Order 1.
2. I would be sufficiently convinced by Order 2.
3. I would be sufficiently convinced in both cases.
4. I would not be sufficiently convinced in either case.

Question 6: Please provide an explanation to the above two answers, using numerical calculations or diagrams if appropriate.

You should indicate, for both Order 1 and Order 2, how convinced you are that Thomas stole the cash, whether you are sufficiently convinced (greater than 70%) that Thomas stole the cash (and thus recommend investigation), and you should discuss how swapping the witnesses may impact your convictions. Better scores are likely to be obtained from a complete and well-reasoned explanation.

Consider the following scenarios:

Order 1: Anne (who claims to have directly observed Thomas) would correctly report evidence of wrongdoing 90% of the time whereas Brenda (who reports Anne’s testimony) would correctly report evidence of wrongdoing only 10% of the time. On the remaining occasions, they would stay silent or mis-report. You receive Brenda’s report of what Anne claims to have seen. Imagine how convinced Brenda’s report would make you that Thomas stole the cash.

Order 2: Imagine that everything about Anne and Brenda stays the same except that they have swapped places, so that it is Brenda who claims to have seen Thomas, and Anne who reports on Brenda’s testimony. Again, imagine how convinced Anne’s report would make you that Thomas stole the cash.

Case Comparison Question

Consider the two cases you have just been presented:

1. Witness statements from (1) Dan via Robert and (2) Robert via Dan.
2. Witness statements from (1) Anne via Brenda and (2) Brenda via Anne.

Question 7: In which of the two cases do you think order made the most difference to the probability of Thomas’s theft?

[Please select from the following options in the study survey]

1. Case 1: Dan and Robert.
2. Case 2: Anne and Brenda.
3. No difference between the two cases.

Please note: In this problem, there are two fictional countries: Ul’Sanda and Rinia. These two countries are not at war, but each is known to carefully monitor the other.

Situation:

You and your Ul’Sandan investigative team have been tasked with assessing whether a temporary Ul’Sandan Black Site (unacknowledged military facility) was observed by foreign surveillance.

The Black Site was located in the middle of a small island off the coast of Ul’Sanda, not visible from the sea. The island is small, remote, and unpopulated; it can safely be assumed that any potential surveillance of the island was airborne.

Crucially, the Black Site team had lookouts stationed at it throughout the day. One of the lookouts reported seeing (and then photographing) some thin, wispy clouds which looked like potential contrails from an aircraft. This raised alarms due to the possibility of a surveillance aircraft having flown overhead. Apart from this, there were no other lookout observations indicating that an aircraft of any sort overflew the island. Of course, there is the possibility that the lookouts missed another aircraft flying over the site.

The site was located on the island for approximately 24 hours, before being moved elsewhere. It is your job to determine the probability that the site was overflown by aerial reconnaissance during that time.

There are a number of possible candidates that may have flown over the island over the period of 24 hours. The two leading candidates, based on the location of the island, and known historical flight paths, are:

1. Rinian Spy Plane: These unmanned aircraft have been known to fly over theareas close to the Ul’Sandan mainland. When the site was moved onto theisland, Ul’Sandan intelligence - based on evidence available at the time(including known flight paths) - concluded that there was a 10% probabilitythat a Rinian spy plane would fly over the island during that 24-hour period. Inthe intelligence community, a 10% probability is taken to mean that an assessed event is highly improbable.



2. Ul’Sandan Drone: Operated by the Ul’Sandan Navy and Air Force, these remote operated aircraft have long-range capabilities, and have been known to follow flight paths that take them over the island. When the site was moved onto the island, Ul’Sandan intelligence - based on evidence available at the time (including known flight paths) - concluded that there was a 5% probability that a Ul’Sandan Drone would fly over the island during that 24-hour period. In the intelligence community, a 5% probability is taken to mean that an assessed event is remote.

Questions:

For your answers, assume the facts to be as stated in the problem.

1. What do you believe is the probability of a Rinian spy plane having overflown the Black Site, referring to all relevant evidence?


2. What do you believe is the probability of a Ul’Sandan drone having overflown the Black Site, referring to all relevant evidence?


3. Which of these two scenarios (Rinian spy plane or Ul’Sandan drone flying over the island) is more likely?


4. Does the report need to recommend notifying counter-intelligence agencies immediately (i.e. is the probability of the Black Site having being overflown by a Rinian spy plane over 50%, having considered the evidence)?

Please provide your reasoning for all responses, referring to the evidence in each case.

List of evidence sources:

You are tasked with evaluating the impact of reports from the following sources:

• Foreign Intelligence Intercepts of Rinian Spy Plane activity
• Ul’Sandan Department of Defence report on Ul’Sandan Drone activit
• Domestic Contrail Expert on Rinian spy planes
• Domestic Contrail Expert on Ul’Sandan Drones
• Radar Station (Technical Report)

Critical purpose of investigation:

There is a pertinent purpose for your investigation: Crucially, if – having evaluated the evidence available to you – you believe the probability of a Rinian spy plane having flown over the island during the 24-hours that the Black site was on the island surpasses 50% (even-odds) by any amount, then you are required to recommend notifying counter-intelligence agencies immediately. If you do not think this probability exceeds 50%, immediate notification is not required and you can postpone communicating your judgment - one way or the other - for up to 48 hours on the possibility that more information may come available.

Rinian Spy Plane Evidence

Evidence 1:

Foreign Intelligence Intercepts

Translated intercepts of Rinian intelligence activities. These are translated, assessed, and summarised by experts on Rinian intelligence and counterintelligence. Due to the possibility of mistranslations, misinterpretations, and the possible sowing of false information, the following statistics on how to consider the uncertainty surrounding reports have been compiled for your use:

Report Reliability Statistics:
False Positive Rate (reporting that activity occurred, when in fact none took place):10%
False Negative Rate (reporting that activity did not occur, when in fact it did take place): 15%

Report Summary:
The report states that, based on intercepted Rinian intelligence transmissions, a Rinian spy plane flew over the island while the Black Site was present.

Rinian Spy Plane Evidence

Evidence 2:

Domestic Contrail Expert on Rinian Spy Planes

A member of your team is an expert on the contrails of Rinian spy planes, and has experience with a large number of prior incidents, so you show the expert the image taken of the potential contrails.

Your teammate’s history of reliability and accuracy reveals, however, that his assessments are not perfect. In particular, verification statistics indicate that this expert is overly bold; frequently proclaiming that suspicious cloud formations /contrails are the contrails of Rinian spy planes when they in fact are not (although he sometimes makes the opposite mistake). Checking the expert’s verified performance statistics you find:

Expert Reliability Statistics:
False Positive Rate (classifying suspicious image as a Rinian spy plane contrail, when in fact it is not): 40%
False Negative Rate (classifying suspicious image as not a Rinian spy plane contrail, when in fact it is): 20%

Report Summary:
The expert reports that, based on his assessment of the image, a Rinian spy plane was not flying over the island at the time the images were captured.

Ul’Sandan Drone Evidence

Evidence 3:

Department of Defense Report

As an Ul’Sandan official, you have access to Ul’Sandan military logs regarding possible flight paths of Ul’Sandan aircraft – including Ul’Sandan drones. These reports can generally be considered to be highly reliable, and the report reliability statistics are taken to be the following:

Report Reliability Statistics:
False Positive Rate (reporting that a certain flight path was followed when in fact it was not): 5%
False Negative Rate (reporting that a certain flight path was not followed when in fact it was the path taken): 5%

Report Summary:
The report states that, based on an assessment of Defence Department logs, a Ul’Sandan drone flew over the island while the Black Site was present.

Ul’Sandan Drone Evidence

Evidence 4:

Domestic Contrail Expert on Ul’Sandan Drones

Contrails of Ul’Sandan drones are quite different from contrails of Rinian spy planes. A member of your team is an expert on the contrails of Ul’Sandan drones, and has experience with a large number of prior incidents, so you show the expert the image taken of the potential contrails.

Your teammate’s history of reliability and accuracy reveals, however, that her assessments are not perfect. In particular, verification statistics indicate that this expert is overly cautious; frequently proclaiming that suspicious cloud formations / contrails are not the contrails of Ul’Sandan Drones when they in fact are (although she sometimes makes the opposite mistake). Checking the expert’s verified performance statistics you find:

Expert Reliability Statistics:
False Positive Rate (classifying suspicious image as an Ul’Sandan drone contrail, when in fact it is not): 20%
False Negative Rate (classifying suspicious image as not an Ul’Sandan drone contrail, when in fact it is): 30%

Report Summary:
The expert reports that, based on her assessment of the image, a Ul’Sandan drone was not flying over the island at the time the images were captured.

Technical Report Evidence

Evidence 5:

Radar Station automated logs

An old radar listening station is located on the island, covering the area of sky above the island’s landmass.

These stations were automated, and were designed to look for particular radar signatures, providing a simple daily report log that indicated positive if anything meeting its target signature characteristics had been detected in the last 24 hours(and negative if nothing had).

Automated Report Log Reliability:
Even now, the automated report logs are considered highly reliable, in that they have very low chances of false positives (0.5%) if no such signatures were present. There is however, an issue with the report logs: Although the radar station was originally designed to look for signatures corresponding to the typical size and altitudes of Rinian spy planes, in more modern times, two types of plane are known to fit these criteria: Rinian spy planes and Ul’Sandan drones. As such, the engineers who maintain the station provide you with the statistics they have regarding typical detection probabilities for each of these two cases:

Ul-Sandan drones have typically triggered positive reports 95% of the time they have been known to fly within the range of the radar, while modern Rinian spy planes have typically triggered positive reports 90% of the time that they are known to be within the area covered by the radar.

Automated Report Log:
The report comes back as positive for the 24-hour period when the Black Site was present.